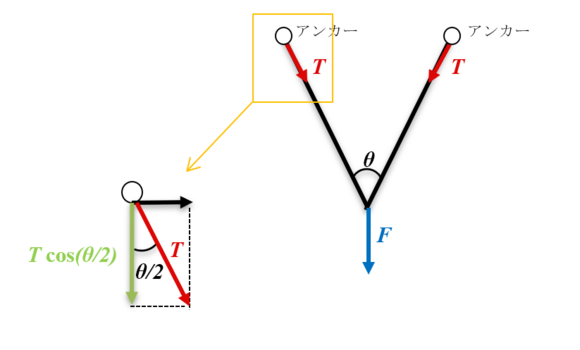
アンカー間の角度
マルチピッチクライミング等で終了点を構築するとき、安全確保のため、基本的には2つ以上のアンカーをスリングで連結します。理由は、①1つのアンカーが仮に抜けたとしてもあと1つは残ることを期待すること、②2つのアンカーを連結することで1つあたりにかかる力を分散すること、の2つです。
②の荷重分散の観点では、アンカー間の 角度 \(\theta\)(図1)は小さいほど良く、逆に角度が広すぎると1本だけで使用するよりも荷重が増幅されてしまいます。
最も荷重分散の程度が大きいのは、\(\theta\) = 0°のときで、各々のアンカーが受け持つ力は半分ずつとなります。現実的にはアンカーが直線上に並んでいることはまれなので、\(\theta\)はある程度の大きさ(30°とか60°とか)になります。
\(\theta\)の変化に応じて荷重がどう変化するかを考えてみます。2つのうち1つのアンカーにかかる張力\(T\)は、図1の左下の図から分かるように、垂直成分は\(T\cos\frac{\theta}{2}\)です。\(T\)の垂直成分2つ分で1つの\(F\)を支えているので、力の釣合いから、
\[2T\cos\frac{\theta}{2} = F\]
ですから、
\[T=\frac{F}{2\cos\frac{\theta}{2}}\]
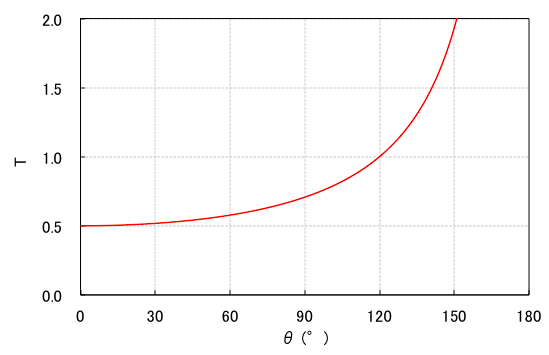
となります。\(F = 1\)として\(T\)と \(\theta\)の関係を示すと図2のようになります。
\(\theta\)が30°くらいまでなら\(T\)はほぼ0.5なので、アンカー1本あたりが受ける荷重は約半分となり、荷重分散の効果は大きいといえます。60°でも0.6くらいですので、60°以下になるようにセットするのが理想的です。60°というのは正三角形の1つの角度なので、アンカーセットにあたっては、正三角形よりも鋭利な三角形をつくるイメージです。
\(\theta\)が90°になると0.7なので、最悪でもこのくらいに収めたいところです。120°では1となって分散効果はなくなります。以降、角度が大きくなるにつれて、単体で使うよりも、アンカー1つあたりに加わる荷重は増えてしまいます。下表に示すように、150°で2倍、175°では12倍、180°に至っては荷重は無限大となってしまいます(が、実際にはスリングに伸びが発生するので、180°になることはありません)。
| 角度θ(°) | \[T=\frac{1}{2\cos\frac{\theta}{2}}\] |
| 0 | 0.50 |
| 30 | 0.52 |
| 60 | 0.58 |
| 90 | 0.71 |
| 120 | 1.00 |
| 150 | 1.93 |
| 175 | 11.5 |
| 180 | ∞ |
まとめ
- アンカー間の角度\(\theta\)が小さいほど、支点への分散効果は大きくなります。
- \(\theta\)は60°以下にするのが理想的。せいぜい90°くらいまで。120°で分散効果は無くなり、それ以上大きな角度になると、むしろ支点への荷重が大きくなるため逆効果です。