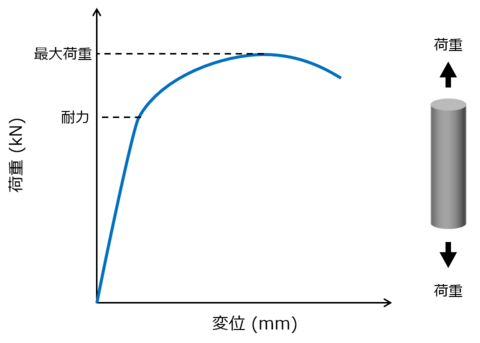クライミング金属材料(4) 弾性変形とカラビナのゲート

ポイント・オブ・ノーリターン

材料の強度のうち、完全に壊れてしまうときの強度というのはイメージしやすいです。前回の記事では、破断荷重について安全率を考察しました。破断荷重を超えてしまうと、金属が破断してしまうので、そのような力を加えてはいけないのは当然でしょう。その他にもう一つ大切な指標として、「耐力（たいりょく）」というものがあります。

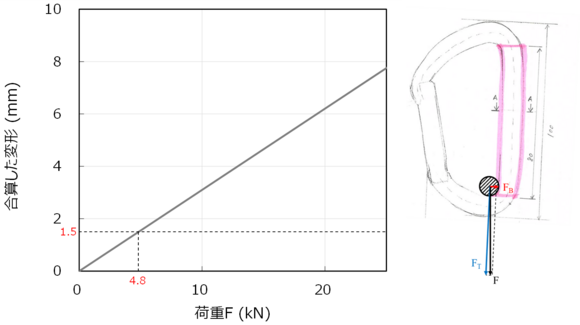
金属材料、例えば図1の丸棒をイメージしてください。丸棒の長手方向に力を加えると、荷重が増えるしたがって少しずつ変形して、変位が増えていきます。そのため、図1の左側にあるグラフのように、縦軸が増えると横軸も増えていきます。その関係は、途中までは直線的で、直線の上限に達するポイントまでは、金属であろうともゴムの様に元に戻ります。直線関係の上限を超えてしまうと、もう後には引けず、荷重の増加に力に応じて変形が残ってしまいます。そして、ついには引きちぎれて破断するのです。

この、直線関係の上限である、過ぎてしまうともう元には戻れないポイント・オブ・ノーリターンの部分が「耐力」です。正確にどの部分の力を耐力とするかは、はっきりと分からないことが多いので、弾性領域の直線を、横方向に0.2%シフトさせたときの交点を基準にする方法が一般的です。これを0.2%耐力と呼び、σ_0.2やσ_YSなどと表記します。

0.2%耐力を超えるまでは、荷重と変位の関係は直線関係にあり、この範囲での変形を「弾性変形」と呼びます。

カラビナのゲート部分の隙間

話は変わって、いつものクライミングに使っているカラビナのゲートを見てみますと、ゲートを閉じたときにカラビナ本体との隙間が空いています。ワイヤーゲート、キーロックのゲート、形は様々ありますが、いずれも隙間が空いています。そりゃそうです、隙間がなければゲートの開閉ができません。でも、接触してなくていいのでしょうか。

カラビナに表示されている強度は、ゲートが開いた状態と閉じた状態とでは随分と違っています。

• 閉じた状態：23kN
• 開いた状態：9kN

ゲートが開いた状態では、閉じた状態の半分以下の強度です。カラビナに荷重がかかる大事な局面になると、カラビナ本体が弾性変形してゲート部分に接触して、荷重が取り除かれると（弾性変形なので）何ごともなかったかのように元に戻っているのでしょうか。Petzl スピリット ストレートを実測してみると、隙間は1.5mmでした。

弾性変形量の推定

引張変形

どれくらいの荷重でどれくらい変形するのか、簡単にモデル化して推定してみます。果たして1.5mmの隙間は弾性変形の範囲で埋まるのでしょうか。カラビナの構造を真面目に考えると難しそうなので、図3の赤マーカー部分のように、直線部分のみの変形量を推定してみます。断面は、大まかな形として台形（上辺4mm、下辺9mm、高さ11mm）とします。

弾性変形の範囲内では、加わった荷重に応じて一定量の変形が生まれ、式(1)のように表せます。

\[E = \frac{\sigma}{\epsilon} \tag{1}\]

ここで、\(\epsilon\)：ひずみ、\(\sigma\)：応力、\(E\)：ヤング率です。ヤング率Eは、とある荷重が加わったときに材料がどれだけ変形するかの係数です。ヤング率の単位は、応力と同じくPa（パスカル）ですが、数値としてすごく大きいのでG（ギガ、メガの1000倍）をつけてGPaで表示することが多いです。

式(1)を変形すると

\[\epsilon = \frac{\sigma}{E} \tag{2}\]

となって、加わった応力に応じてどれだけの変形量（ひずみ量）が発生するのかを推定することができます。式(2)によると、ひずみ量を求めるために必要な情報は、応力とヤング率です。応力は荷重と断面積から決まります。ヤング率は、材質によって決まり、クライミング用品に用いられているアルミニウム合金の場合は約70GPaです。これらの値を使って計算してみます。

ゲートを閉じた状態のカラビナの耐荷重は23kNとあるので、この半分以下、10kNの荷重を加えてみましょう。まず、このときの応力\(\sigma\)を求めます。

\[\sigma = \frac{荷重}{断面積} = \frac{10000}{(4+9)*11/2} = 140\]

応力は140MPaとなりました。つぎに、140MPaの応力が加わったときのひずみ\(\epsilon\)を求めます。

\[\epsilon = \frac{\sigma}{E} = \frac{140}{70000} = 0.002\]

ひずみは0.002です。想定している80mmの長さに対して0.002変形するということなので、変形量（伸び）は80×0.002 = 0.16mmとなります。荷重と引張方向の伸びをグラフ表示したのが図4です。

直線部分のみを真っ直ぐ引張った際の変形量というのは、ゲート部の隙間1.5mmを埋めるほどではないということですね。

曲げ変形

引張変形だけではゲート部の隙間を埋めるほど変化しないことが分かりましたので、次は、曲げによる弾性変形を考えてみます。引張と同様に、変形の推定にはヤング率と断面積と荷重が関係します。引張と違うのは、曲げる部分の長さや曲げる部分の断面形状も関係する点です。

引張の場合、応力だけを考えればよかったので、形状として必要な情報は断面積のみでした。曲げの場合は、断面積だけでなく、断面形状が丸なのか四角なのかH型なのかということも影響してきます。最近のカラビナの断面形状は3次元的に連続的に変化して複雑な形をしています（20年くらい前の製品は円形断面が多かったです）。手計算で正確に表現するのは難しいので、引張のときと同じように、近似的にすべて台形であると仮定しておきます。

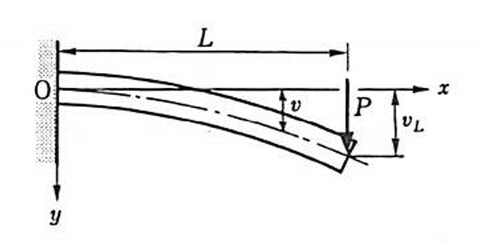
曲げ変形をどう評価するか、考え方は色々とありますが、最も簡単な方法として、片側が固定されたはり、いわゆる「片持ちはり」であると考えます。

材料力学の教えるところによると、梁の先端に集中荷重Pが加わった場合の変形量vは式(3)で計算されます^[1]吉田 総仁, 弾塑性力学の基礎,  共立出版, 1997.。

\[v = \frac{PL^3}{3EI} \tag{3}\]

ここで、L：はりの長さ、E：ヤング率、I：断面二次モーメントです。断面二次モーメントというのが、断面の形状によって変わる値です。便覧などで各種形状の計算方法が整理されていますし、計算サイトも多いので、台形の断面二次モーメント計算のサイトを活用させていただきました。想定している上辺4mm、下辺9mm、高さ11mmの台形では、断面二次モーメントは685mm⁴となります。

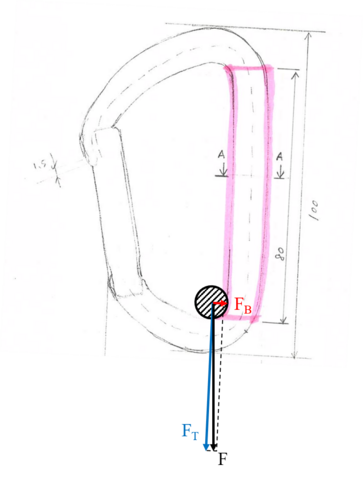
曲げに影響する荷重がどれくらい加わっているのかは正確に知ることは難しいですが、鉛直方向（真下の方向）に力が加わったときに、若干カラビナが傾いて、真横の成分が生まれると考えてみます（図6）。仮に傾きが5°であるとすると、

\[F_B = F\sin(5^\circ) = 0.09F\]

となります。10kN真下に引かれるとすると曲げ変形分は10×0.09 = 0.9kNとなります（なお、このように力を分解した場合は、引張変形分はF cos(5°) = 0.996Fなので、10×0.996で9.96kNとなります。ほとんど変わらないです）。

では、式(3)に各値を入力して、曲げ変形量vを計算してみます。

\[v = \frac{PL^3}{3EI} = \frac{900\times80^3}{3\times70000\times685} = 3.2\]

3.2mmの変形量となりました。引張よりもはるかに少ない荷重で、それなりの曲げ変形が生じることが確認されました。例えば茹でる前のスパゲティを長手方向に引張ってもほとんど変形しませんが、曲げると容易に変形するので、直感的なイメージとも合っているかと思います。

引張＋曲げ変形量の合成

せっかくなので、引張＋曲げの変形量を合成してみます。これまで考えてきたのは、図8の右下部分、カラビナのストレート部分下端の変形量でした。例えば10kNのときには、引張変形は0.16mm、曲げ変形は3.2mmでした。それぞれ、方向は直交しているので、これらを合成するには三平方の定理から

\[合算した変形 = \sqrt{引張変形^2 + 曲げ変形^2} = \sqrt{0.16^2 + 3.2^2} = 3.2 \]

となり、合成した変形量はほぼ曲げのみで決まり、約3.2mmです。この変形量が、そのまま左上のゲート部の隙間まで伝わると仮定すると、ゲート部の隙間1.5mmは、10kNの荷重が加わったときには埋まっているので、密着した状態になっていると考えられます。

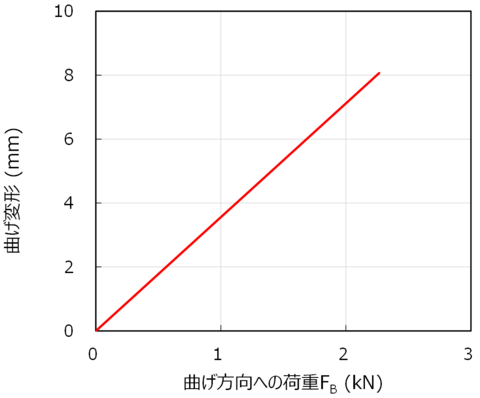
合算した変形量を荷重（ロープによって下向きに引かれる荷重）毎に計算してグラフ化したものが図9です。この図によると、ゲート部の隙間1.5mmの変形が生まれるのは、4.8kNの荷重が加わったときです。

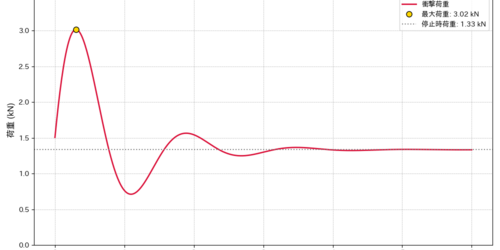
4.8kNというと、約480kgの重さをゆっくり吊り上げたときの力に相当しますから、人がゆっくりぶら下がったときにはまだ隙間は空いていることになります。クライミング中にフォールしたときのように、衝撃的に荷重が加わると4.8kNを超える可能性は十分にあり得ます（例えば、クライマーが70kgだとしすると下側に引かれる力は2倍の140kgf、衝撃荷重によって4倍になるとすると560kgf）。そのようなときには、ゲート部の隙間がピッタリと閉じ、カラビナ全体で隙間のない金属リングのような状態になっていると推定されます。

また、このときの応力は、

引張応力 = 荷重/断面積 = 4800/71.5 = 67 (MPa)
曲げ応力 = 曲げモーメント/断面係数 = (421×80)/(253) = 133 (MPa)

です。多くのカラビナの材質として使用されているアルミニウム合金7075 T6の0.2%耐力は500MPa程なので、ゲート部の隙間が密着する段階では弾性変形（塑性変形しない）範囲内にあることも確認できました。

したがって、カラビナに荷重がかかる大事な局面になると、カラビナ本体が弾性変形してゲート部分に接触して、荷重が取り除かれると（弾性変形なので）何ごともなかったかのように元に戻っていると思われます。

まとめ

金属材料の性質の一つとして、弾性変形についてみてきました。例題として、カラビナのゲート部の隙間1.5mmが、カラビナに荷重が加わったときに弾性変形で埋まるのかどうかを、弾性変形の知識を使って検討しました。カラビナの直線部分のみに引張荷重が加わるという単純化したモデルでは、ゲート部の隙間1.5mmを埋めるほどには変形しない結果となりました。曲げによる弾性変形も考慮すると、弾性範囲内でゲート部の隙間は埋まると推定されました。

シリーズ一覧

• クライミング金属材料