クライミング時の衝撃力(3) 衝撃力の意味

前回の記事では、リードクライミングで実際にフォールしたときの衝撃荷重を、確保理論の式から予測される値と比較しました。今回は、衝撃力とは何かを少し探っていきます。

力とは何か

衝撃力の前に「力」を考えます。重たい物を持ち上げると重たいと感じますし、乗っている自動車が急に曲がると横方向に力を受けます。これらはいずれも「力」です。動いていない物から感じる力、動いている自動車の中でだけ感じる力、どちらも確かな力です。

偉大な物理学者であるニュートンは、現実世界の規則性を追求する過程で、力（記号\(F\)とします）は、質量（記号\(m\)とします）と加速度（記号\(a\)とします）を使って、

\[F = ma \tag{1}\]

で表現できることを見出しました。これをニュートンの運動方程式^[1]崎間, 運動方程式1, 物理のかぎしっぽ, 2005と言います。質量に加速度を乗じた数値が力であるということです。加速度とは、速度の速度とでもいうか、速度が変化する割合です。

自動車が急カーブを進むとき、カーブに沿って動く方向が変わる（加速度が生じる）ので力が発生します。急発進、急停車するときも速度が変化する（加速度が生じる）ので力が発生します。

では、重たい物を持ち続けているときにも力を感じるのはなぜでしょうか。沢山買い物した帰り道では、エコバッグの持ち手が指に食い込みます。物は特に加速していないのに、力を感じます。

実は、物体が動いていない（静止している）ときには、地球の重力による加速度が働いています。加速度が働いているので、力が生まれているという塩梅です。重力による加速度には、重力加速度という名前が付けられていて、その大きさは約9.81m/s²（メートル毎秒毎秒）です。

例えば、体重5.5kgの猫が座っているときに床に与える力は、5.5kg×9.8m/s^2 = 約54kg・m/s^2という大きさになります。質量に重力加速度を掛けた値にはN（ニュートン）という国際単位がありますので、このときの力は54Nと書けます。

ニュートンという力の単位は、カラビナなどに24kNなどと刻印されているので、僕たちクライマーにはおなじみの単位です。

衝撃力とはなにか

猫が静かに座ったり寝たりしている限りは、床には54Nの力が加わっています。しかし、猫が高い場所からジャンプして床に着地した瞬間はどうでしょう。いかに猫がしなやかでも、瞬間的に54Nよりも大きな力が発生します。これが衝撃力です。言い換えれば、物体の速度が短時間に変化するときの力が、衝撃力です。

このような関係を表すために、運動量と力積という量があります（高校で物理学を学んだ人は、聞いたことがあるでしょう）。力積\(F\Delta t\)（\(F\)は力、\(\Delta t\)は短い時間）は、運動量\(mv\)（\(m\)は質量、\(v\)は速度）の変化に等しい、という運動量保存則があります。式で書くと、

\[F\Delta t = m(v_0 – v_1) \tag{2}\]

となります。ここで、\(v_0\)が最初の速度、\(v_1\)がぶつかったあとの速度です。

少し想像してみます。運動量は質量\(m\)と速度\(v\)を掛けた量なので、同じ速度であっても、質量が大きい程、運動量は大きくなります。

体重5.5kgの猫が走ってこちらに向かって来た可愛らしいですが、体重30kgの大型犬が同じ速度で走ってきたら一抹の不安を感じることでしょう。なぜなら運動量が約5倍も大きいからです。運動量とは、動く物が持っている勢いというかスゴ味のようなものです。

衝撃力の話をしていたのでした。式(2)の左側の\(F\)、これが衝撃力です。右側は運動量の変化ですが、極端なケースとして、\(v_1\)がゼロになるとしましょう。すると、

\[F\Delta t = mv \tag{3}\]

とシンプルになります。さらに両辺を\(\Delta t\)で割ると

\[F = \frac{mv}{\Delta t} \tag{4}\]

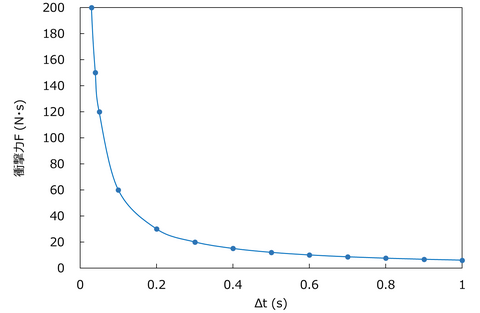
になります。これは何を意味しているでしょうか。こういうときは、何か仮の数字を代入してみて何パターンか値を計算してみるとイメージが湧きます。\(m\) = 6kg、\(v\) = 1m/sとして、\(\Delta t\)をいくつか変えてグラフにしてみました。

衝突時間Δtが小さいと衝撃力は大きくなり、衝突時間Δtが大きくなるほど、急激に衝撃力は小さくなります。

一瞬でズバンとぶつかると衝撃力が大きそうですし、ゆっくりふわりと衝突なら、衝撃力も小さくて済みそう、というイメージに合致すると思います。

運動量保存則から導出された確保理論

クライミングでの墜落時の荷重も運動量の関係から知ることができそうです（確保理論の式はエネルギー保存則によるもの）。調べてみると、Miura氏によって導出されていました^[2]三浦, 落下係数, 2013.。

落下による位置エネルギーから初速度\(v\)が求まり、速度がロープの伸びによって線形的に減少して、とある時間をかけて速度が0になるとして\(\Delta t\)を求め、

\[F = \frac{2mg}{r}\frac{h}{L} \tag{5}\]

から衝撃力\(F\)が推定されます。ここで、m：体重、g：重力加速度、r：ロープ伸び率、h：落下距離、L：ロープ長さです。

僕は、落下係数によって衝撃力が決まるというのはちょっと不思議だったのですが、こうして運動量の考え方、すなわち\(\Delta t\)が大きければ衝撃力は小さくなる、という原理を考えることで納得しました。

つまり、長い距離を墜落して位置エネルギーの変化が大きかったとしても、その分ロープが長い距離伸びるので、びよよんとロープが衝撃を吸収してくれる時間も長くなって停止までの時間が稼げるので、落下係数（落下距離をロープ長さで割った値）で整理できるのでしょう。

そういう意味では、制動確保でロープを流すダイナミックビレイも同じ原理に基づくもので、衝突中の時間を稼ぐことで、衝撃力を減らそうとする技術なのだろうと思います（ちなみに意図的にロープを流して適切に止めるのはかなり難しいので僕にはできません）。

まとめ

力とはなにか、衝撃力はなにかを考えることで、衝撃力は運動量の変化から理解することができました。ロープの伸びと停止までの時間の関係を、もう少し理論的に推定できれば面白そう、ということで次回に続きます。