クライミング時の衝撃力(2) リードの墜落
自作した計装化クイックドロー(荷重計測可能なクイックドロー)をひっぱり出し、リードクライミング中にフォールしたときの衝撃荷重を実測しました。その計測結果と、確保理論で予想される値とを比較してみます。
衝撃荷重の実測
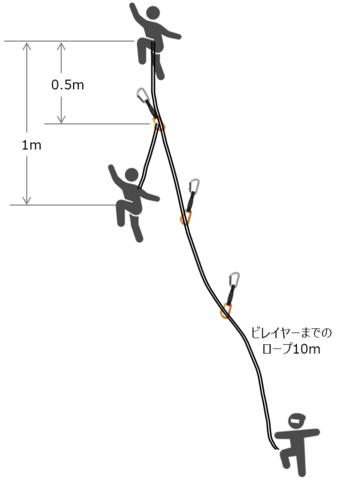
長さ15m程のルート(グレードは5.9)の2/3辺りのボルトに計装化クイックドローをセットし、ボルトから約0.5m登った位置でクライマーが墜落し、そのとき支点に加わる計測しました。クライマーの体重は75kg(装備含めて80kg)です。
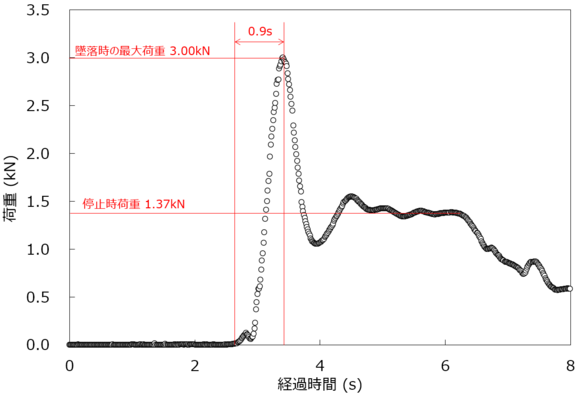
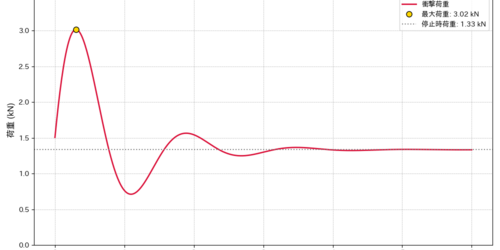
取得したデータの時間(秒、s)と荷重(キロニュートン、kN)の関係を整理したのが下図です。クライマーは僕で、自ら墜落するというのはけっこう怖かったのですが、こうして墜落時の荷重を時刻歴で取得できたので頑張った甲斐がありました。
墜落時の最大荷重は3.00kN、静止時の荷重は1.37kNでした。サンプリング周波数は50Hzなので、ピークを捉えきれていない可能性はあるものの、この結果に基づいて考察しみます。
確保理論に関する文献
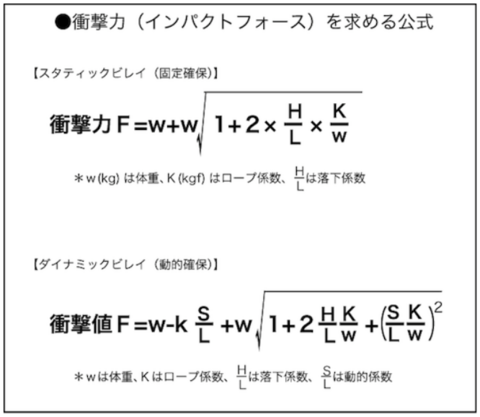
クライミングの入門書などを読むと「確保理論」なるものが出てきます。衝撃力は墜落距離に依らず、墜落するロープの長さと受け止める側のロープの長さの比で決まるというものです。確保理論といえばまず行き着くのが確保理論テキスト[1]国立登山研修所 確保理論テキスト研究会編, 確保理論テキスト, 2012.です。衝撃力を推定する2つの式が記載されています。
これらの式から衝撃力を求めるには、ロープ係数が必要になりますが、確保理論テキスト中に、(計算例に2000kgfという値は出てくるものの)ロープ係数についての説明はありません。なお、スタティックビレイの式の導出過程は、Attawayの1996年の論文[2]S. Attaway, “Rope System Analysis”, 1996.に詳しく記載されています(位置エネルギーが、運動エネルギーとロープの弾性エネルギーに変換され、ロープの最大張力が衝撃力であるとして導出)。
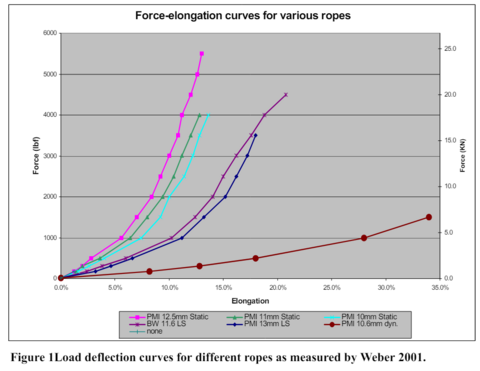
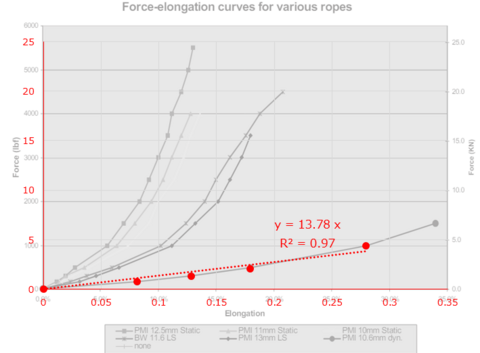
ロープ係数についてネットを探し回ると、ロープ種類(スタティック、ダイナミック)やロープ径別に、ロープの伸びと力の対応を整理した図が見つかりました[3]S. Attaway, C. Weber, “Predicting Rope Impact Forces Using a Non-linear Force Deflection”, International Technical Rescue Symposium, 2002.。
この傾きが、ロープ係数に他なりません。図中の「PMI 10.6mm dyn.」がシングルのダイナミックロープに近いと思いますので、この値を使用することにします。なお、PMIとは、レスキュー用品メーカーのようです(日本ではあまり馴染みがありませんね)。
プロット点をデジタイザで読み取り、線形フィッティングして傾きを求めたのが下図です。ここで、ロープの伸びが30%を超えると線形関係から外れてしまうので、約28%の点まででフィッティングしました。得られたロープ係数は約13.8kNです。10%伸ばそうと思ったら1.38kNの力が必要、ということです。
ちなみに、この論文[3]の趣旨は、ロープ係数を線形で近似すると衝撃荷重を非保守側に扱う可能性があるので2次関数でフィッティングした方が良いというものですが、10.6mmのダイナミックロープの特定範囲でのみであれば線形関係が成立していそうなので、ここではロープ係数が一定であるとして扱います。
実測値と確保理論の比較
計算のための準備が一応は整いましたので、確保理論と今回の実測値を比較してみます。簡単のため、スタティックビレイの式を用います。
\[F = W + W\sqrt{1 + 2\frac{HK}{LW}} \tag{1}\]
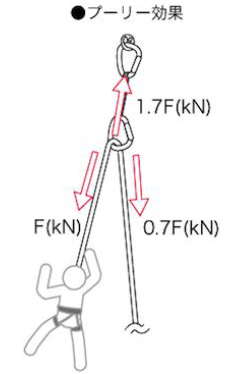
今回行った実験では、支点に加わる荷重を計測しました。式(1)で求められるFは、墜落したクライマーが受ける力です。支点には、ビレイヤー側のロープによる力も加わります。確保理論テキストによると、ビレイヤー側には0.7倍の荷重が加わる(プーリー効果)とされているので、クライマー側と合わせて合計1.7Fの力となります。
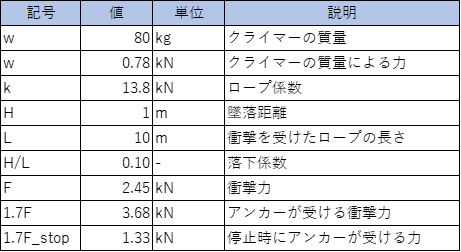
以上を考慮して、アンカーが受ける衝撃力を計算してみると3.68kNとなりました。実測値は3.00kNでした。確保理論から予測されるピーク荷重に比べ、実測値は20%程低めです。
確保理論による計算には、いくつか仮定*1があることを考慮すると、さほど悪くないかな、という印象です。
*1 今回仮定したこと:
・ロープ係数は文献値を使用
・墜落距離と衝撃を受けたロープの長さは概算値
・厳密なスタティックビレイではない
停止時の荷重は1.33kN(自重の1.7倍)と推定され、実測値は1.37kNでしたので、確保理論テキストのプーリー効果は概ね正しそうです。
まとめ
自作のデータローガーでクライミング中の衝撃荷重を実測した結果と、確保理論から推定される値とを比較しました。確保理論から予測されるピーク荷重に比べ、実測値は20%程低めになっており、より正確な推定にはロープ係数その他の前提条件をより正確な値とする必要があるものの、大まかには理論値と対応しているようでした。