クライミング時の衝撃力(4) 減衰振動
リードクライミングで墜落した時の衝撃力に関する検討の続きです。前回の記事では、墜落したクライマーの勢いを表す物理量である運動量(質量×速度)と、衝撃力の尺度である力積(力×作用時間)との関係から、衝撃力は「運動量」を「停止までの時間で割ったもの」として表せることを示しました。
今回は、クライマーが停止するとき、ロープに衝撃が吸収される過程での経時変化を扱ってみます。
ロープの役割
リードクライミングにおいて、ロープがあるからこそ、墜落しても(基本的には)地面に衝突する前に停止します。止まる瞬間に、ロープがぐいーんと伸びてくれるからこそ、衝撃が吸収されます。
クライミングで用いられるロープには、大きく分けて「ダイナミックロープ」と「セミスタティックロープ」の2種類があります。両者の違いは、力を加えたときの伸び量です。これを伸び率と言い、例えば100kgの人がぶ5mのロープにぶら下がったら5.5mの長さになった場合、元の5mに対して0.5m伸びたことになるので、10%の伸び率となります。
ダイナミックロープでは伸び率が30%以上であるのに対し、セミスタティックロープの場合は伸び率が3%程で、10倍もの差があります。よく伸びるのがダイナミックロープ、あまり伸びないのがセミスタティックロープです。
リードクライミングで使われるのはダイナミックロープ(よく伸びる方)です。セミスタティックロープ(伸びにくい方)は、ロープを固定して登り返す時や、荷物を引き揚げる用途で使われます。
減衰振動
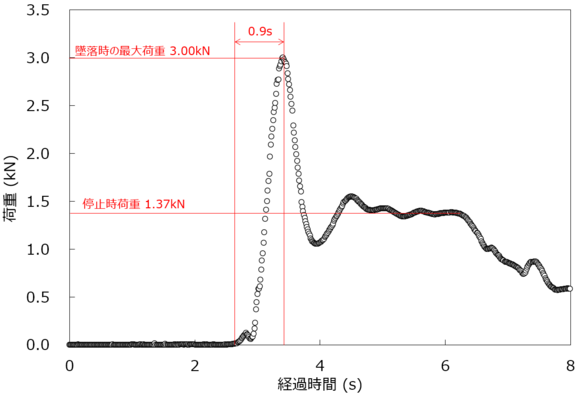
さて、僕が自ら墜落して実測したデータを再び確認してみます。よくデータをみると、荷重が時間に対して波打っている(振動している)ことが分かります。
さらに、その振幅は時間とともに小さくなっています。このような動きは、減衰振動(げんすいしんどう)と呼ばれます。減衰とは、時間が経つにつれて小さくなる、ということです。
確保理論の式では、ロープをばねとして扱い、ロープ定数を導入することで、リードクライミング時の衝撃荷重を推定できました。しかしその方法で推定できるのは最大荷重のみで、そこに至るまでや至った後の時々刻々の変化までは予測できませんでした。
どうにかして、時刻歴も含めて墜落事の挙動を推定できないだろうか、ということを考えてみます。
基礎式
今回は、やや高度な(より一般化された)運動方程式に登場してもらいます。僕もよく分かっている訳ではないのですが、巨人の肩に立つべく、物理の教科書にある知識を、えいやっと活用します。
加速度aは、位置xの2階の時間微分ですので、(そういうものがあるのだと一旦飲み込んで)微分方程式として表します。
$$ m\ddot{x} = F $$
ここで、いつものごとくmは質量で、Fは力です。xは位置を表していて、上に2つ点が着いていることは時間の2階微分(加速度)であることを表しています。
さらに、クライミングロープを、衝撃吸収能力を備えたバネとして表現します。バネ定数をkとすると、位置xに比例して力が加わることになるので、
$$ m\ddot{x}+kx= F $$
と表せます。最初の式にkxが加わっただけです。
ここからさらに、「減衰」という項目を追加します。いろいろな先人達の結果から、減衰は減衰係数dと位置xについての1階微分(速度)の積として表されることが分かっています。式で書くと
$$ m\ddot{x}+d\dot{x}+kx= F $$
という具合です。一つ前の式に\( d\dot{x} \)が加わっただけです。自然科学の素晴らしいところは、このように、現象の背後にある基本的な概念を数式として表現できることです。
基礎式を解く
基礎的な方程式に落とし込んでしまえば、あとはこれを解くだけです。このような問題は古今東西の優秀な方々が挑戦し答えを導き出しているので、それを真似れば僕のような素人でも答えを知ることができます。
微分方程式で表された関係を現実問題にフィードバックするには、積分操作を行います。積分というのは、答えがない場合も多いので、コンピュータの力を借りて数値計算し、近似的な答えを求める方が簡単な場合が多いです。
計算を始めるためには、初期状態を決める必要があります。今回の計算では、「ロープがピンと張って伸び始める瞬間」を時刻 t=0 とします。その時の条件を、以下のように設定します。
- 初期速度 \( \dot{x}(0) \): クライマーが自由落下してきた速度。今回は1mの高さから墜落したときの速度 \( \sqrt{2gh} \)とします。
- 初期位置 \( x(0) \): ロープはまだ伸びていないので0とします。
あとは、数値計算で解いていきます。計算に使ったPythonコードをGitHubで公開していますので、詳しくはそちらを御覧ください。計算の結果、下図が得られました。
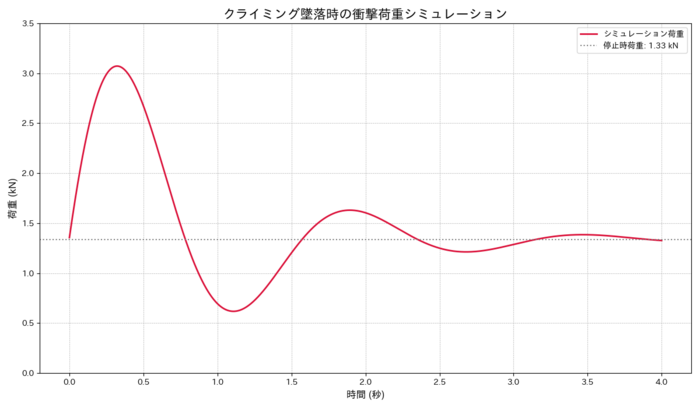
このグラフは、実測データで見たような、大きなピークの後に何度か振動して、最終的にクライマーの体重に相当する荷重に収束していく様子が良く再現できていると思います。ロープの「ばね」としての性質(ばね定数k)だけでなく、「減衰」の性質(減衰係数d)を考慮することで、最大荷重に至るまでや至った後の時々刻々の変化を表現できるようになりました。
実測データと一緒にプロットしてみましょう。
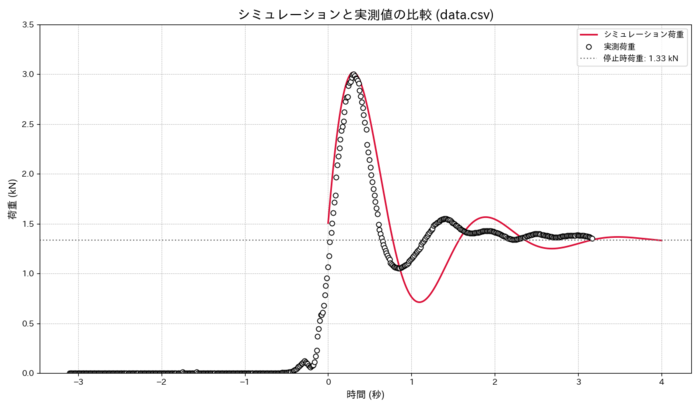
最初の波型はだいたい合ってます。ただし、減衰係数dの値が不明だったので、ピーク荷重がだいたい一致するように合わせこんで200 N・s/mとしました。また、横軸は実測とシミュレーションのピーク位置が同じになるように基準位置のみをスライドして合わせています。
減衰の度合いは実測の方が早いので、実際には減衰係数dは一定値ではなく、ロープの伸びに応じて変動しているのではと思います。
まとめ
リードクライミングでの墜落を「減衰振動」という物理モデルで捉え、最大衝撃力だけでなく、衝撃が加わってから収束するまでの荷重全体の時間変化をシミュレーションしました。実際の墜落はもっと複雑な要素が絡み合いますが、ロープの性能を「ばね定数 k」と「減衰係数 d」という2つのパラメータで表す単純なモデルでも、墜落してロープが衝撃を吸収する過程をけっこう上手く説明できることが分かりました。